此篇文章貌似没有重点,日常笔记吧。
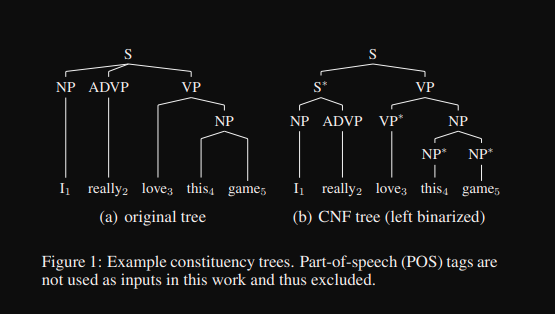
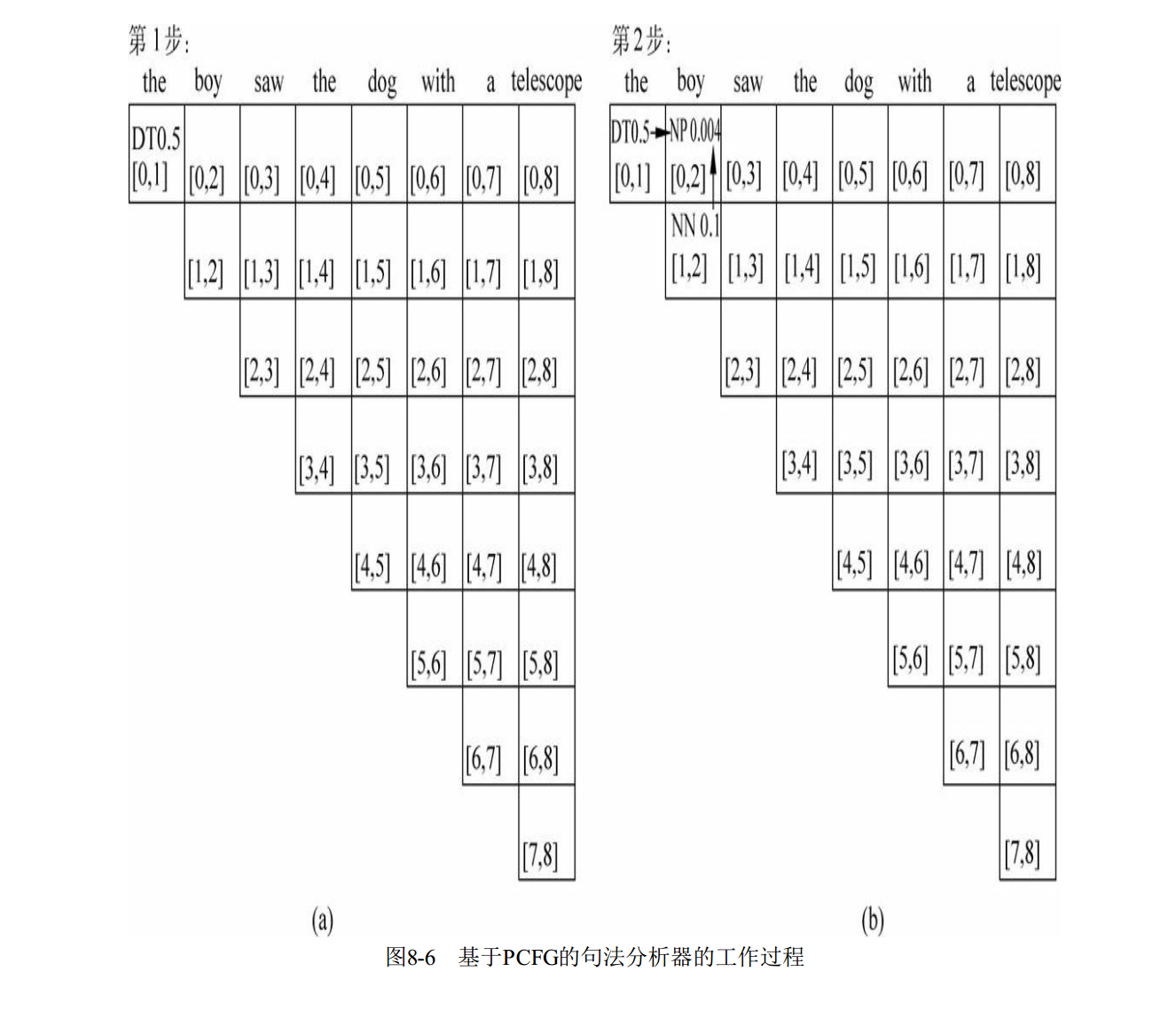
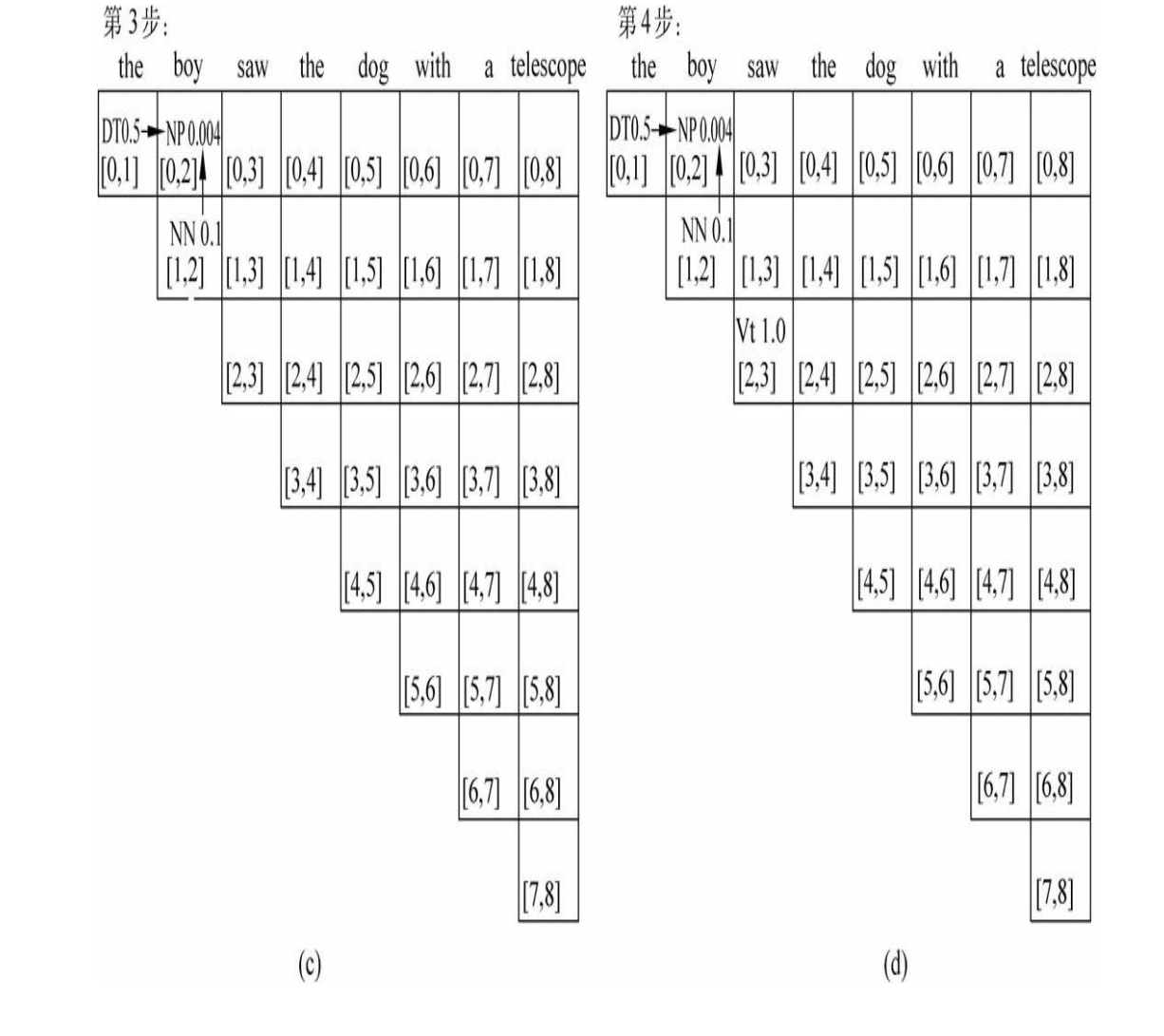
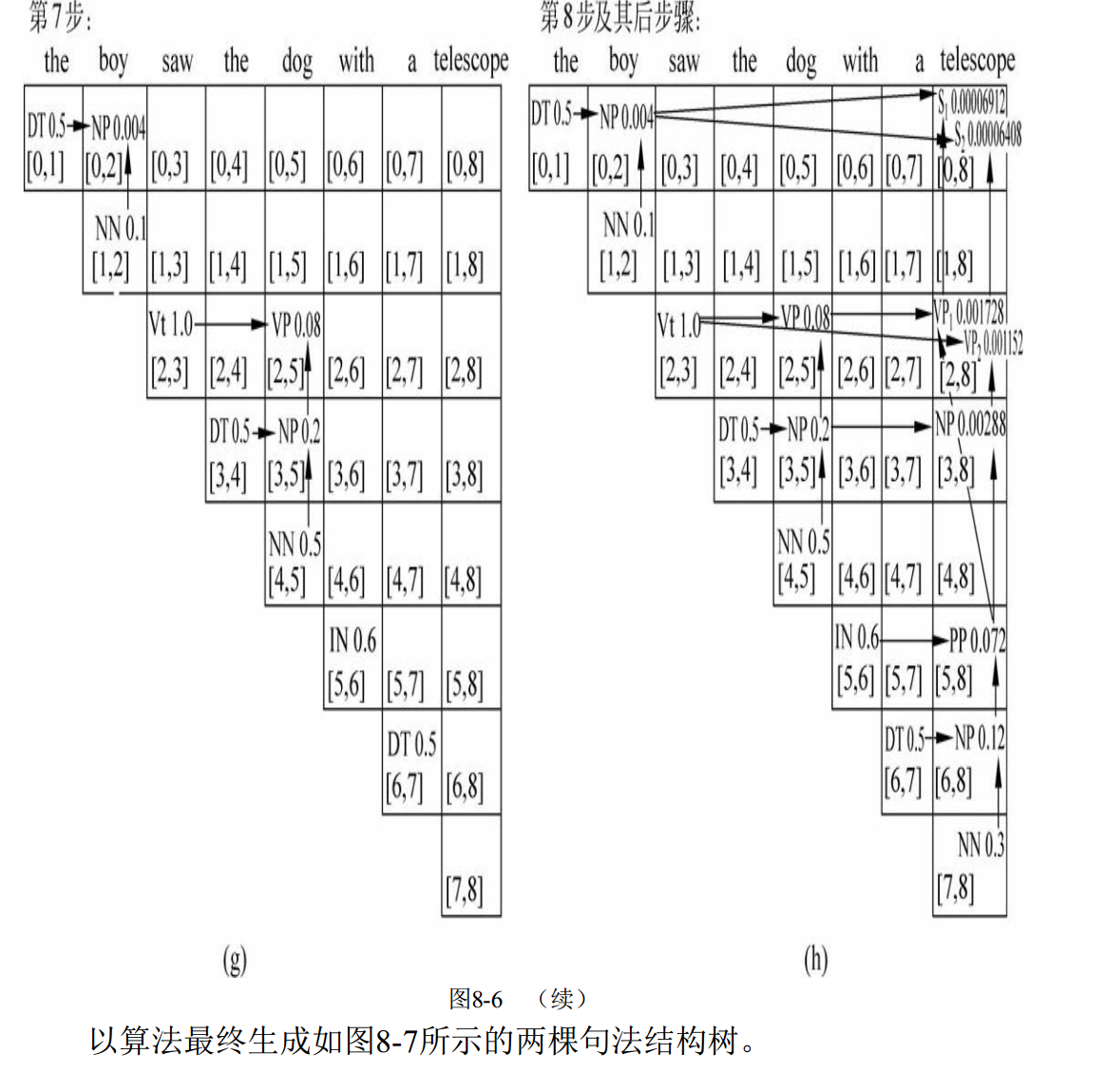
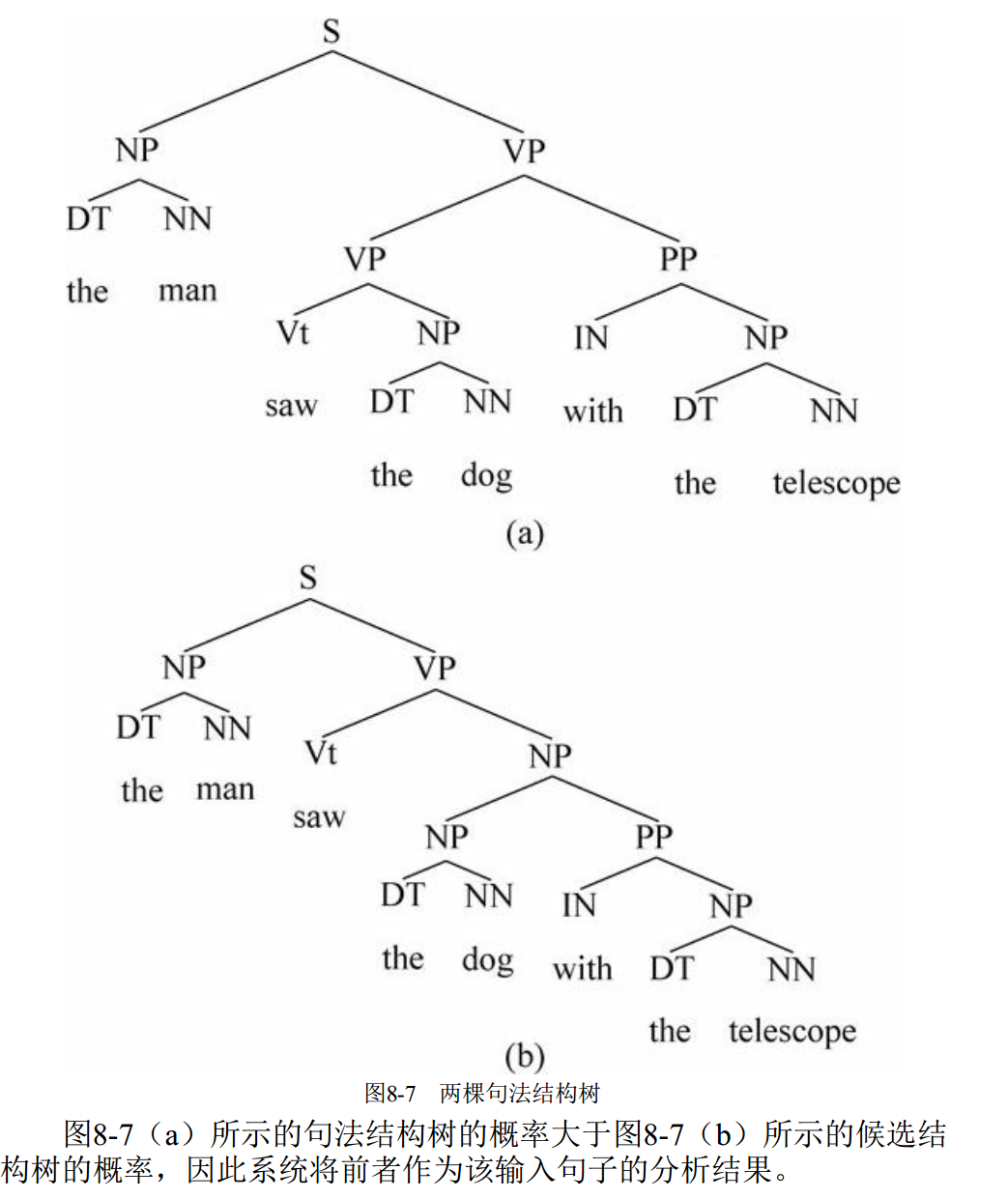
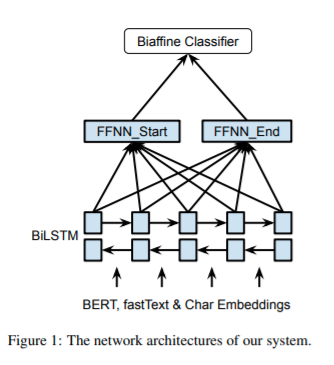
基于树形条件随机场的高阶句法分析作者硕士毕业论文,关于句法分析的历史与实现基本讲了一遍,包括作者使用TreeCRF高阶建模等工作。
代码,这个项目包含了句法分析任务的实现。包括dependency parser,semantic dependency parser,constituency parser等。
对于句法分析工作,百度ddparser相比下来可能是工业上更好的选择,不过目前个人更倾向于语义句法工作,相比下来更接近直观感受(还是看任务啦~)。
不管是semantic role labeling(语义角色标注)或者semantic dependency parser(语义依存分析),看ltp的演示效果。
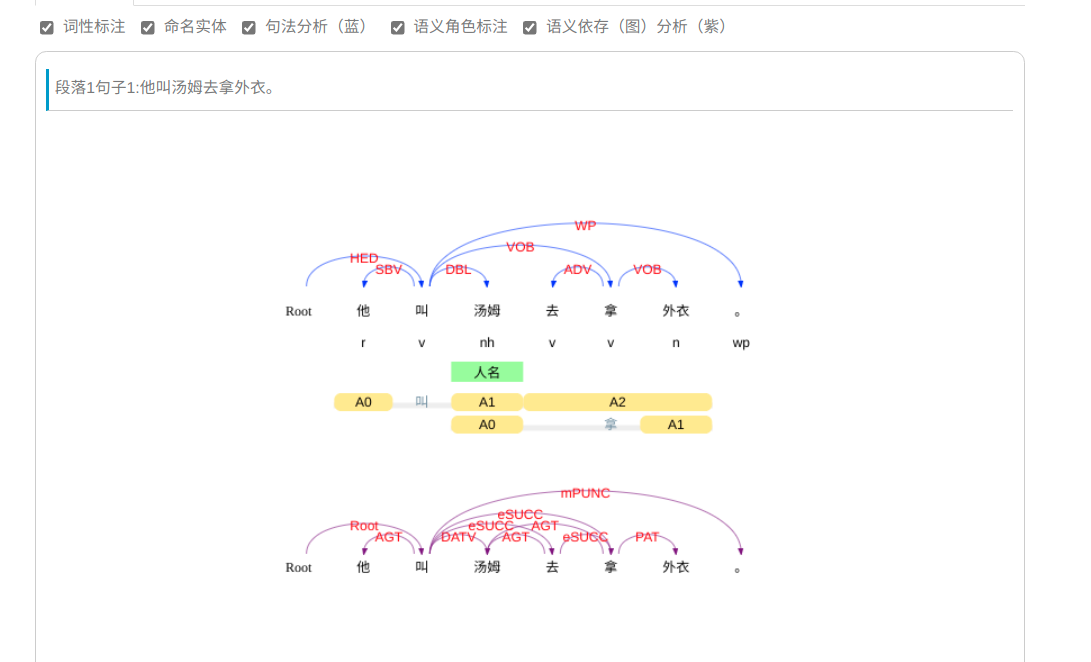
但是不能光看这种效果,从目前公开的论文水平来看,准确率并没有很高,另外高质量,高数量的标注数据集也相对少。
大家都是一样的模型,比的就是数据集喽,这点不得不夸HanLP,至少人家代码里面都有数据集,方便学习。