1. 什么是条件随机场
条件随机场是一种给定输入随机变量x,求解条件概率p(y|x)的概率无向图模型。用于序列标注任务时,会特例化为线性链条件随机场。此时输入和输出序列为等长。
2. 为什么需要条件随机场
对于序列标注任务,此类任务有分词、词性标注等,本质是对每一个字(假设bert做特征提取)进行预测,然后接全连接层进行softmax激活,如下图所示:
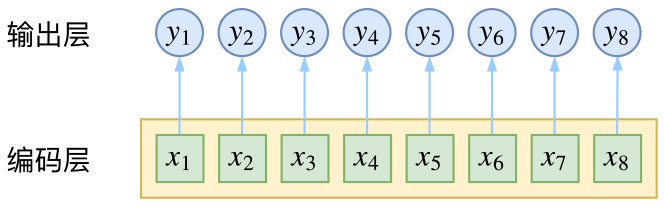
以词性标注任务来讲,x表示观测序列,y表示预测序列,即词性分布。
按照中文使用规律来讲,动词后面接动词的可能性基本不存在(或者对于分词任务来讲蝴后面基本就是蝶),而在上述模型中,观测序列没有考虑彼此之间的关联。
对于一个长度为n的句子,一共有m个词性,那么一共有m * n个可能性。
crf引入了预测序列的关联,并以路径为单元,预测m^n个可能性中求最优的路径。
3. 如何求解loss值
在计算下面条件概率时,引入了以下几个假设进行简化计算:
1 | P(y1,…,yn|x1,…,xn)=P(y1,…,yn|x),x=(x1,…,xn) |
计算简化
- 假设该分布呈指数族分布
- 输出之间是相邻位置关联的
- 发射概率通过rnn进行获取
对其进行-log,变成相加问题,求其最大似然估计。
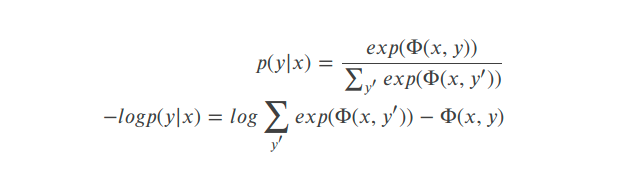
其中:
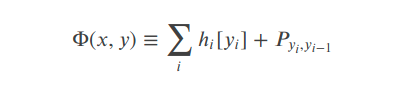
这个函数前一部分表示rnn到输出(标签)的发射概率矩阵,后一部分表示相邻标签的状态转移概率矩阵。
第一部分获取上述公式的计算结果,即分子项的计算结果,为目标的序列的打分结果。计算函数
第二部分是要求解分母项,需要在所有可能的路径上进行打分进行指数求和。计算函数
因为只考虑临近项,那么就可以递归的求出归一化因子,使用动态规划的方式获取所有路径的得分指数和。
4. 预测
在计算好的状态转移矩阵和发射概率矩阵,使用viterbi算法获取序列的最优路径解。
5. 有向无环图的求解(延展)
viterbi算法不是为nlp所生的,求解最优路径也有其他的算法,比如dijkstra,prim等。但是本质区别在于viterbi是动态规划算法,后两者属于贪心算法,计算资源消耗更多。另外动态规划本质是空间换时间。
关于viterbi动态规划求解,求解步骤如下:
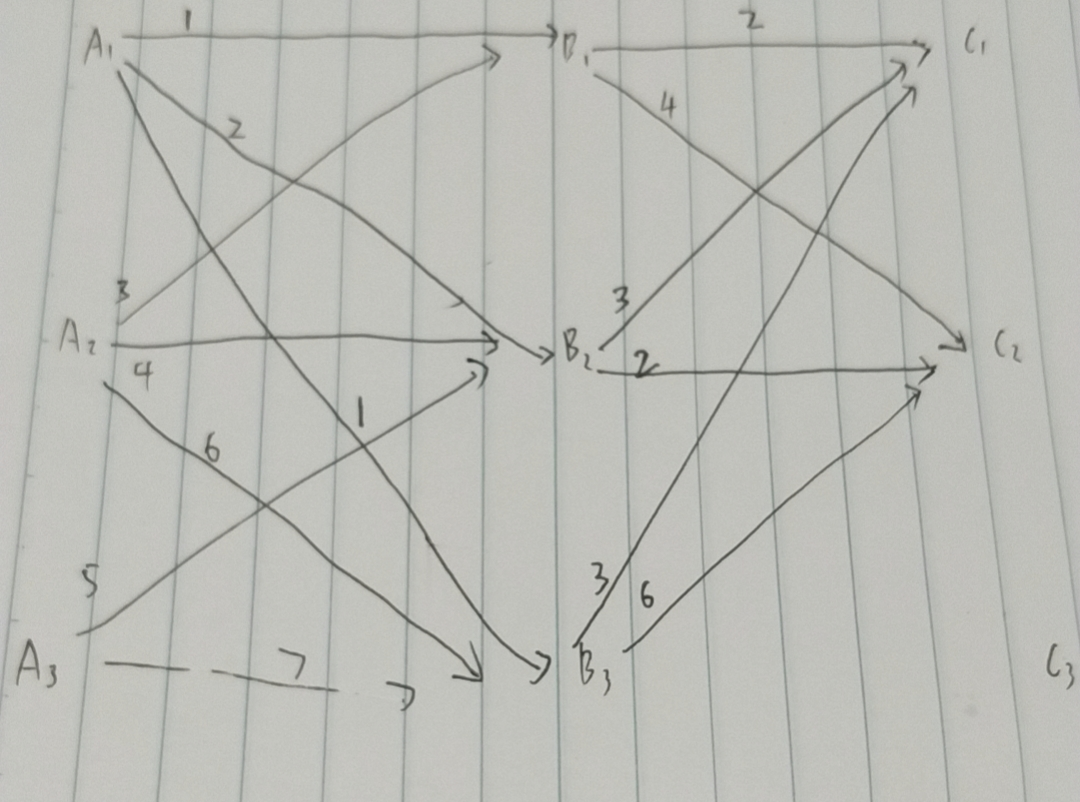
从最左边开始,
A1,A2,A3都是起点,A1 -> B1为1, A2 -> B1为3,A3 -> B1(我擦,漏了。。假设为4),那么A1,A2,A3到B1的最短路径为1(即A1 -> B1)。
同理得到B2的最短路径为2(即A1->B2),到B3的最短路径为1(A1->B3)。
从B1,B2,B3到C1的最短路径为2(即B1 -> C1),到C2的最短路径为2,(B2 -> C2),后续忽略。那么得到下张图:
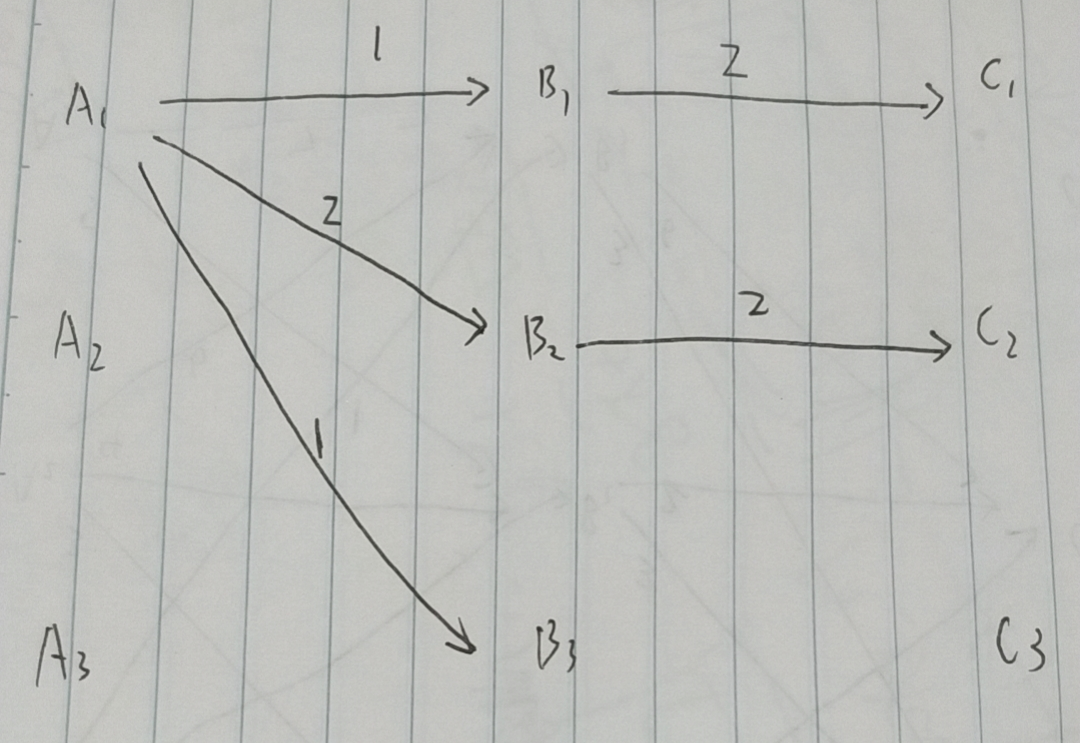
可以看出,到C1最短路径为(A1 -> B1 -> C1),到C2最短路径为(A1 -> B2 -> C2)。
至此,求解过程完毕。
