介绍隐马尔可夫

2020-06-16

什么是马尔可夫性质？

“……一个随机过程，在这个过程中，鉴于现在，未来独立于过去。”

假设一个带有公平硬币的简化抛硬币游戏。暂停怀疑并假设马尔可夫性质尚不清楚，我们想预测 10 次翻转后翻转正面的概率。在条件依赖的假设下（硬币具有过去状态的记忆，未来状态取决于过去状态的顺序），我们必须记录导致第 11 次翻转的特定顺序以及这些翻转的联合概率。所以想象在 10 次翻转后，我们有一个随机的正面和反面序列。该序列的联合概率为 0.5^10 = 0.0009765625。在条件依赖下，下一次翻转的概率为 0.0009765625 * 0.5 = 0.00048828125。

这是第 11 次翻转的真实概率吗？一定不行！

我们知道，抛硬币的事件并不取决于之前抛硬币的结果。硬币没有记忆。连续翻转的过程不会对先前的结果进行编码。每次翻转都是一个独特的事件，正面或反面的概率相等，也就是有条件地独立于过去的状态。这就是马尔可夫性质。

什么是马尔科夫模型？

马尔可夫链（模型）描述了一个随机过程，其中未来状态的假设概率仅取决于当前过程状态，而不取决于它之前的任何状态（shocker）。

让我们进入一个简单的例子。假设您想对给定当前状态的狗处于三种状态之一的未来概率进行建模。为此，我们需要指定状态空间、初始概率和转移概率。

想象一下你有一只非常懒惰的胖狗，所以我们将状态空间定义为睡觉、吃饭或大便。我们将初始概率分别设置为 35%、35% 和 30%。

import numpy as np
import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline

# create state space and initial state probabilities

states = ['sleeping', 'eating', 'pooping']
pi = [0.35, 0.35, 0.3]
state_space = pd.Series(pi, index=states, name='states')
print(state_space)
print(state_space.sum())

下一步是定义转移概率。它们只是在给定当前状态的情况下保持相同状态或移动到不同状态的概率。

q_df = pd.DataFrame(columns=states, index=states)
q_df.loc[states[0]] = [0.4, 0.2, 0.4]
q_df.loc[states[1]] = [0.45, 0.45, 0.1]
q_df.loc[states[2]] = [0.45, 0.25, .3]

print(q_df)

q = q_df.values
print('\n', q, q.shape, '\n')
print(q_df.sum(axis=1))

现在我们已经设置了初始和转移概率，我们可以使用Networkx 包创建一个马尔可夫图。

要做到这一点，需要一点灵活的思维。Networkx 创建由节点和边组成的图。在我们的玩具示例中，狗的可能状态是节点，边是连接节点的线。转移概率是权重。它们表示在给定当前状态的情况下转换到某个状态的概率。

需要注意的是 networkx 主要处理字典对象。话虽如此，我们需要创建一个字典对象来保存我们的边及其权重。

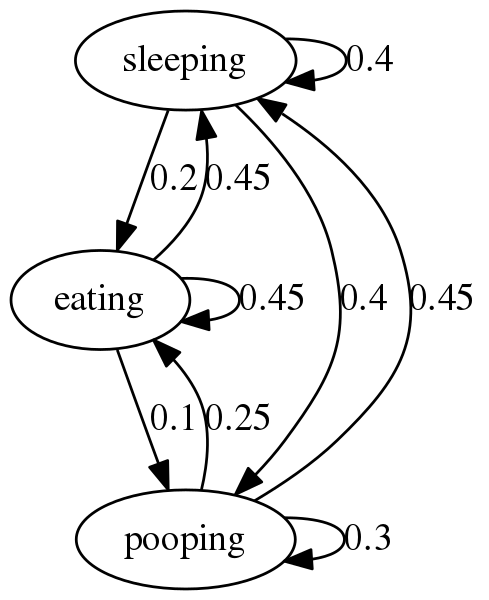
不错。如果你沿着任何节点的边走，它会告诉你狗转换到另一个状态的概率。例如，如果狗在睡觉，我们可以看到狗有 40% 的机会继续睡觉，40% 的机会狗醒来并拉屎，20% 的机会狗醒来吃东西。

什么是马克可夫隐藏状态

考虑这样一种情况，您的狗行为异常，并且您想对狗的行为是由于疾病或其他方面健康时的古怪行为进行建模的可能性。

在这种情况下，狗的真实状态是未知的，因此对您隐藏。对此进行建模的一种方法是假设狗具有代表真实隐藏状态的可观察行为。让我们来看一个例子。

首先，我们创建我们的状态空间——健康或生病。我们假设它们是等概率的。



hidden_states = ['healthy', 'sick']
pi = [0.5, 0.5]
state_space = pd.Series(pi, index=hidden_states, name='states')
print(state_space)
print('\n', state_space.sum())


a_df = pd.DataFrame(columns=hidden_states, index=hidden_states)
a_df.loc[hidden_states[0]] = [0.7, 0.3]
a_df.loc[hidden_states[1]] = [0.4, 0.6]

print(a_df)

a = a_df.values
print('\n', a, a.shape, '\n')
print(a_df.sum(axis=1))

这是它变得更有趣的地方。现在我们创建发射或观测概率矩阵。该矩阵的大小为 M x O，其中 M 是隐藏状态的数量，O 是可能的可观察状态的数量。

给定当前的可观察状态，发射矩阵告诉我们狗处于隐藏状态之一的概率。

让我们保持与上一个示例相同的可观察状态。狗可以睡觉、吃东西或大便。现在我们做出最好的猜测来填充概率。

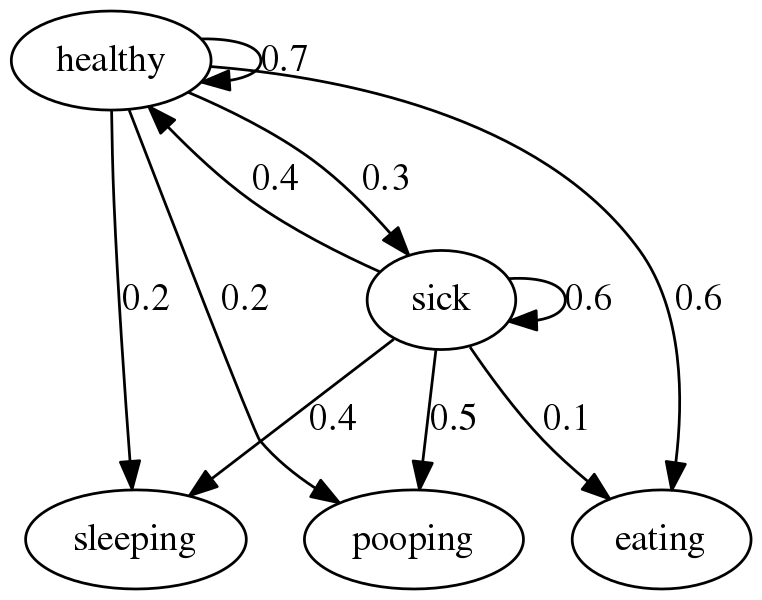
看这个图时，将healthy和sick作为同一level,从sleeping，pooping, eating到healthy和sick的边就是发射概率。

隐马尔可夫图稍微复杂一些，但原理是相同的。例如，您会预期，如果您的狗正在进食，那么它健康的可能性很高 (60%)，而生病的可能性非常低 (10%)。

现在，如果您需要根据一系列观察结果随着时间的推移辨别您的狗的健康状况怎么办？

使用Viterbi 算法，我们可以根据观察序列确定最可能的隐藏状态序列。

高的水平，在每个时间步长Viterbi算法的增量，寻找最大的是得到陈述的任何路径的概率我在时间牛逼，那也有序列最多时间正确的观察牛逼。

该算法还跟踪每个阶段概率最高的状态。在序列的末尾，算法将向后迭代，选择每个时间步“获胜”的状态，从而创建最可能的路径，或可能导致观察序列的隐藏状态序列。

最终代码：


# -*- coding: utf8 -*-

import numpy as np

import pandas as pd



def viterbi(pi, a, b, obs):
    """Viterbi algorithm for solving the uncovering problem

    Notebook: C5/C5S3_Viterbi.ipynb

    Args:
        a (np.ndarray): State transition probability matrix of dimension I x I
        pi (np.ndarray): Initial state distribution  of dimension I
        b (np.ndarray): Output probability matrix of dimension I x K
        obs (np.ndarray): Observation sequence of length N

    Returns:
        path (np.ndarray): Optimal state sequence of length N
        delta (np.ndarray): Accumulated probability matrix
        E (np.ndarray): Backtracking matrix
    """
    n_states = a.shape[0]  # Number of states
    T = len(obs)  # Length of observation sequence

    # Initialize D and E matrices
    delta = np.zeros((n_states, T))
    E = np.zeros((n_states, T - 1)).astype(np.int32)
    delta[:, 0] = np.multiply(pi, b[:, obs[0]])

    # Compute D and E in a nested loop
    print('start walk forward'.center(30, '-'))
    for n in range(1, T):
        for i in range(n_states):
            temp_product = np.multiply(a[:, i], delta[:, n - 1])
            delta[i, n] = np.max(temp_product) * b[i, obs[n]]
            E[i, n - 1] = np.argmax(temp_product)
            print('s={s} and t={t}: phi[{s}, {t}] = {phi}'.format(s=i, t=n, phi=E[i, n - 1]))

    # Backtracking
    print('start backtrace'.center(30, '-'))
    path = np.zeros(T).astype(np.int32)
    path[-1] = np.argmax(delta[:, -1])
    for n in range(T - 2, -1, -1):
        path[n] = E[int(path[n + 1]), n]
        print('path[{}] = {}'.format(n, path[n]))
    return path, delta, E




states = ['sleeping', 'eating', 'pooping']
pi = [0.35, 0.35, 0.3]
state_space = pd.Series(pi, index=states, name='states')

q_df = pd.DataFrame(columns=states, index=states)
q_df.loc[states[0]] = [0.4, 0.2, 0.4]
q_df.loc[states[1]] = [0.45, 0.45, 0.1]
q_df.loc[states[2]] = [0.45, 0.25, .3]

q = q_df.values

hidden_states = ['healthy', 'sick']
pi = np.array([0.5, 0.5])
state_space = pd.Series(pi, index=hidden_states, name='states')

a_df = pd.DataFrame(columns=hidden_states, index=hidden_states)
a_df.loc[hidden_states[0]] = [0.7, 0.3]
a_df.loc[hidden_states[1]] = [0.4, 0.6]

a = a_df.values

observable_states = states

b_df = pd.DataFrame(columns=observable_states, index=hidden_states)
b_df.loc[hidden_states[0]] = [0.2, 0.6, 0.2]
b_df.loc[hidden_states[1]] = [0.4, 0.1, 0.5]

b = b_df.values

obs_map = {'sleeping': 0, 'eating': 1, 'pooping': 2}
obs = np.array([1, 1, 2, 1, 0, 1, 2, 1, 0, 2, 2, 0, 1, 0, 1])
inv_obs_map = dict((v,k) for k, v in obs_map.items())
obs_seq = [inv_obs_map[v] for v in list(obs)]

path, delta, phi = viterbi(pi, a, b, obs)
print('\nsingle best state path: \n', path)
print('delta:\n', delta)
print('phi:\n', phi)


state_map = {0:'healthy', 1:'sick'}
state_path = [state_map[v] for v in path]

print(pd.DataFrame()
 .assign(Observation=obs_seq)
 .assign(Best_Path=state_path))

结果：


------start walk forward------
s=0 and t=1: phi[0, 1] = 0
s=1 and t=1: phi[1, 1] = 0
s=0 and t=2: phi[0, 2] = 0
s=1 and t=2: phi[1, 2] = 0
s=0 and t=3: phi[0, 3] = 0
s=1 and t=3: phi[1, 3] = 1
s=0 and t=4: phi[0, 4] = 0
s=1 and t=4: phi[1, 4] = 0
s=0 and t=5: phi[0, 5] = 0
s=1 and t=5: phi[1, 5] = 1
s=0 and t=6: phi[0, 6] = 0
s=1 and t=6: phi[1, 6] = 0
s=0 and t=7: phi[0, 7] = 0
s=1 and t=7: phi[1, 7] = 1
s=0 and t=8: phi[0, 8] = 0
s=1 and t=8: phi[1, 8] = 0
s=0 and t=9: phi[0, 9] = 0
s=1 and t=9: phi[1, 9] = 1
s=0 and t=10: phi[0, 10] = 1
s=1 and t=10: phi[1, 10] = 1
s=0 and t=11: phi[0, 11] = 1
s=1 and t=11: phi[1, 11] = 1
s=0 and t=12: phi[0, 12] = 1
s=1 and t=12: phi[1, 12] = 1
s=0 and t=13: phi[0, 13] = 0
s=1 and t=13: phi[1, 13] = 0
s=0 and t=14: phi[0, 14] = 0
s=1 and t=14: phi[1, 14] = 1
-------start backtrace--------
path[13] = 0
path[12] = 0
path[11] = 1
path[10] = 1
path[9] = 1
path[8] = 1
path[7] = 0
path[6] = 0
path[5] = 0
path[4] = 0
path[3] = 0
path[2] = 0
path[1] = 0
path[0] = 0

single best state path: 
 [0 0 0 0 0 0 0 0 1 1 1 1 0 0 0]
delta:
 [[3.00000000e-01 1.26000000e-01 1.76400000e-02 7.40880000e-03
  1.03723200e-03 4.35637440e-04 6.09892416e-05 2.56154815e-05
  3.58616741e-06 5.02063437e-07 7.37725866e-08 2.21317760e-08
  1.59348787e-08 2.23088302e-09 9.36970868e-10]
 [5.00000000e-02 9.00000000e-03 1.89000000e-02 1.13400000e-03
  8.89056000e-04 5.33433600e-05 6.53456160e-05 3.92073696e-06
  3.07385778e-06 9.22157333e-07 2.76647200e-07 6.63953280e-08
  3.98371968e-09 1.91218545e-09 1.14731127e-10]]
phi:
 [[0 0 0 0 0 0 0 0 0 1 1 1 0 0]
 [0 0 1 0 1 0 1 0 1 1 1 1 0 1]]
   Observation Best_Path
0       eating   healthy
1       eating   healthy
2      pooping   healthy
3       eating   healthy
4     sleeping   healthy
5       eating   healthy
6      pooping   healthy
7       eating   healthy
8     sleeping      sick
9      pooping      sick
10     pooping      sick
11    sleeping      sick
12      eating   healthy
13    sleeping   healthy
14      eating   healthy

Process finished with exit code 0